Vortex dynamics

 

 



 

So far I have presented a phenomenological analysis of the observational data and described the factual nature of the ways the structures in the universe may form, evolve and break up in different scales - starting from the sizes of the stars to the superclusters. The factual evidences show that the universe is built in a hierarchical manner, where the small and the large structures bear much similarities in their growth, breakup and reformation. What appears in the larger scales repeat in the smaller scales. The larger structures are only a collection of similar structures in smaller dimensions.

Thus the universe appears to be a fractal, where the phenomena in the micro-scales are inseparably interlinked with the events happening in the macro-levels. The phenomena happening globally and locally are intricately tied together to form an extremely complex arena of events. However, amidst this extreme complexity the universe bears a universal geometric characteristic, which is revealed as a fractal design. It remains unchanged at different scales of observations.

What is the dynamics, which has created this fractal universe? The fractal characteristic is in contradiction with the big-bang model, which is based on the assumption of homogeneity and isotropy. In fact, it abandons the possibilities of understanding the universe by using differential geometry, which has been the main mathematical apparatus in building the modern cosmology.

If we have to leave the big-bang cosmology, which has dominated science for so many decades, can one find any model which could explain the fractal nature as well as describe why the structures in the cosmos grow, evolve, breakdown and eject as they do?

In fact, the characteristics of turbulence have much similarities with the phenomena which are seen in relation to the structure formation in the universe.The turbulences in fluid or gaseous media may develop due to several causes like mixing, slow dispersion of one media into another, or resistance faced by the moving liquid or gas by an object on the way. They may also be caused by the flows at different temperatures, or speeds coming from different directions and encountering each other. There are also turbulences created by gushing of streams or currents in fluids, plasma, air, or fire, for example. The stream gushing at high velocity roll up the laminar sheets forming the medium, where the streams try to force their ways. More the sheets roll up more resistance are developed in the media, and the sheets roll into thinner and thinner filaments. These filaments may split, bifurcate, coil around or entangle each other while forming knots, or they may also fragment into pieces. Thus a fully developed turbulence will appear as a filamentary soup of coiled and entangled vortices. However, these filaments do not remain stable for a longer period of time. They undergo constant changes of shapes as well as fluctuations of motions. The filaments split, join, merge and break again and again creating a field of motions which may appear chaotic everywhere. In spite of this apparent chaos, the fully developed turbulences, in any media, follow universal characteristics which can be described as geometric objects called multifractals.

For example, the turbulence, which is generated by external forcing like the gushing of stream setting the fluid in churning motions, can be modeled as whorls inside whorls inside whorls and so on: The bigger whorl is made of smaller whorls, which in turn are made of even smaller whorls, which is made of even smaller whorls. Thus turbulence is made of self-similar structures at smaller and smaller scales. The energy which inflow at the larger scale cascades to smaller and smaller dimensions. Different models of turbulence vary depending on the assumption how the energy is injected from the mother structure to its daughter structures, and how the daughter structures may feed back to the mother structures in return.

 

How a turbulence works is not properly understood. Before describing its dynamics I shall first give an analysis of turbulence by visual studies of the motions of the filaments and the knots which develop in a turbulent medium. After that I shall come back to the question how these motions may be governed by the evolutions, tightening, breakdown and formation of knots.

As said, the most characteristic feature of turbulence is its multifractal nature. A fractal is a geometric object, in which self-similar geometric patterns are embedded in smaller and smaller scales. Fractals are simpler objects than the multifractals. In a fractal network of void and matter, if one scoops up an area of certain dimension, from anywhere from the network, one will find similar amount of matter and void in every samples, which defines the measures of the fractal. However, in a multifractal it will be different. Instead of the whole fractal showing the same measure everywhere, the areas of similar measures will form different fractal sets. A multifractal will be a collection of such sets. While a fractal possesses a unique fractional dimension, a multifractal is characterized by a generalized dimension, where different fractal sets are described by their singularity strengths, which correspond to specific fractional dimensions.

The turbulence is not any homogeneous fluid. The distinction between a homogeneous model and the real world can be described as the differences which exist between a clear soup, and the soup containing complexly entangled noodles which form knots around fish balls, or meet balls immersed in that soup. If we pursue the imagery of this Chinese noodle soup, the turbulence is made of noodles of different sizes varying from very thin to thick ones. In fact, the thick noodles are made of coiling of the thinner noodles. The thinner noodles in turn are made of the coiling of the even thinner noodles, which are made of even thinner noodles and so on. The noodles (the filaments) constantly tear, break, split and join again and again as the motions of the turbulence stir the medium. During this stirring the noodles may shrink, or fatten, or form knots, or break away from entanglements.

As I have said before, turbulences can be generated by different means. What I shall analyze in this chapter is mainly the turbulence generated by an external forcing and maintained by a constant supply of energy from outside, like a vortex created by a waterfall at the mouth of a mountain-river. The water running out of the spatially confined vortex which pours out the flows joining into a river is replenished by the water entering into the vortex from the waterfall. With this example I shall demonstrate how the turbulence cascade, feedback and sustains a unique dynamics of the formation and breakdown of knot structures.

The purpose of this analysis is to show how the structures seen in a turbulence resemble closely to the structures one observes in the cosmos. I shall present evidences which will indicate that there may exist a hidden order behind the apparently chaotic motions. I shall also propose that a fractal network acts as the geometrical foundation behind the process, which oscillates between order and chaos.

 

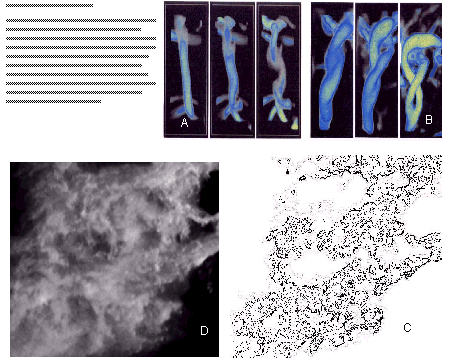
The filaments, which form in the turbulence, follow the hidden fractal pattern and arrange themselves to create the geometrical foundation behind chaos. This fractal is made of self similar pattern at smaller and smaller scales. When flows through all scales are visualized together, the turbulence appears extremely complex, and the motions of any test particle moving in it become intractable. However, the turbulence is not so unpredictable as it may seem in the beginning. The underlying hidden pattern acts as the controller of all motions. It decides the destinies of the flows in all scales. Though there may occur constant fluctuations throughout the system, the turbulence, where the dissipation is constantly replenished by equal amount of incoming flows, maintains a stable geometric structure. While the singularity strengths of the filaments may change with time at a local region, new filaments appear through splitting or merging of filaments, and the process seem to follow a predictable manner. The breakdown, or merging happen in order to serve a global purpose of maintaining the fractal pattern in hierarchically descending scales. Thus the average flow through a local region is not really ad hoc. It has a definite purpose of creating a fractal velocity field, and establish relations with the motions occurring globally in other places in the system.

 

 

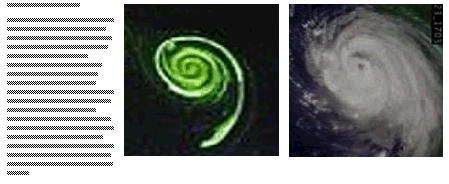
Moreover, there seems to exist a mechanism of energy storage and release by the methods of merging and fattening of the filaments, and then break down of the fattened structures into thinner filaments. As the spiral vortex, shown above, grows and intensifies it follows the universal mechanism irrespective of the media, and the mechanisms of their formation. With the intensification of the vortex the number of windings increases. Together with the increasing number of coiling, one can also observe an oscillatory behavior. One can see merging of thinner filaments into thicker structures. After a certain thickness is reached the fattened filaments split into thinner filaments once again. It appears like an expansion. After the expansion, the thinner filaments start merging together in order to form thicker structures once more and the system appears to contract. As the vortex intensifies and grows this oscillation between expansion and contraction is observed as a universal phenomenon pertaining to the dynamics of turbulence.

 

 

 

 

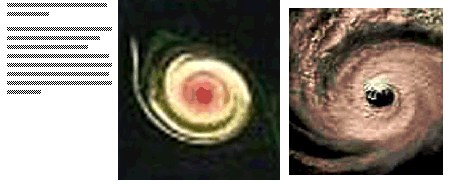
The fractal pattern is made of innumerable vortices. These vortices arrange themselves in a way that the general dynamics of motions of fluids, observed at different scales, may remain similar. The big vortices feed the daughter structures while the daughter structures feed back to their mother structures. In the spiral vortex, as seen in a hurricane or a whirlpool, when the clouds, or the water swirl towards the eye of the vortex, they move towards the center by displacing clouds or water from inside. This displacement appears as outward motions of clouds or fluid emerging from inside to outside. This is the general way how the daughter structure feeds back to the mother structure. The outflowing fluid or the clouds from the daughter scale merge with the inflowing streams of the mother structure, which spiral towards the centre again. This phenomenon is generally known as the cooling flow returning towards the center. The mother structure, in the same manner as its own daughter, repeats the process of feedback outward which cools and then returns to supply incoming flows to its mother structure, while it spirals inward. Thus the same process repeats again and again in scales after scales, and the general dynamics of motions follow a predictable order.

However the globally interconnected flow pattern is woven in an extremely complex manner where, at every moment, filaments everywhere in all scales break, merge, split, coil, fragment again and again creating a scene of chaos.

In the context of the studies of the cosmic structures, the shapes formed due to vortex merging have also resemblances with what one observes in the universe. The merging of vortex pairs of similar strengths, which rotate in the same direction, generate a fractal structure, which involve two bow-shaped envelopes. These dual envelops are hierarchically embedded in descending scales. The hierarchical embedding form shapes like Yin and Yang, which is very similar to what one sees in the cosmic structures. The merged vortices also follow the same universality as the single spiral vortices. Irrespective of the media and the nature of their formations, when vortices merge they generate a universal geometric pattern.

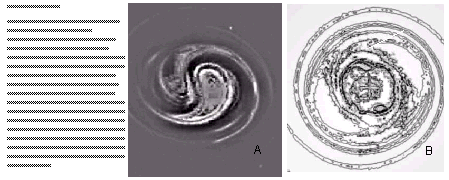
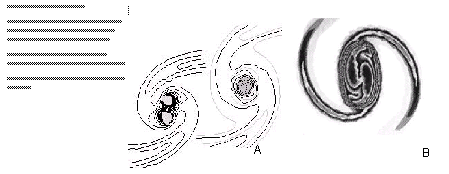
Only a few vortices generate stable geometric shapes. These shapes are created by complex entanglements of filaments and smaller vortices. When seen at higher resolution the simple geometric shape reveals an extremely complicated entanglement. Each of the smaller vortices, which participate in forming the complexity, in turn, are made of similar complex entanglements of filaments and vortices of even smaller dimensions. This hierarchically embedded complexities are characteristics of all vortices in nature.

The filaments and the vortices, forming the geometric pattern, evolve constantly with the passage of time, and create everchanging fluctuations of motions through out the entire pattern.

 

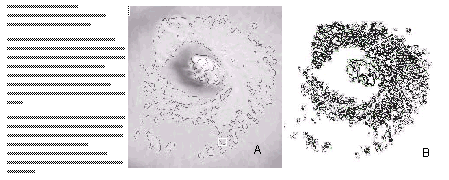
Though the individual filaments and vortices undergo constant evolutions with time, the directions of average flow of fluid through the geometric element remain predictable. The evolutions of the vortices, which are entangled in the network, create fluctuations throughout the pattern. In spite of these fluctuations, there exists clear directions along which inflows and outflows should occur. The ways the outflowing streams embolden the inflowing streams and, in turn, inflowing streams split to join the outflowing streams follow a universal rule. This rule repeats in all vortices which create the same geometric pattern. Though the path of a test particle, moving in the vortex, can not be predicted beyond a very short time, the global movements of the streams follow rather predictable paths. One can predict the way the vortices and the filaments will entangle, and the average motions of flow at different parts of the geometric element by studying the geometry alone. Thus there exists a predictable global order behind an unpredictable local chaos.

 

 

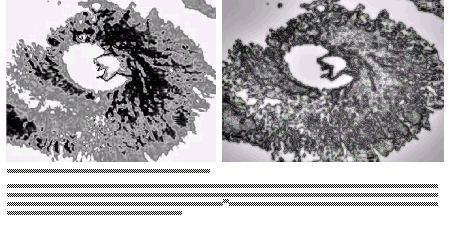
One may ask why do the flows through the never changing geometric pattern are everchanging? I have already said that it is caused by the evolutions of the vortices and the filaments which weave the network hiding the order. Why do the filaments and the vortices evolve? What causes them to grow? As I have explained earlier, when more and more streams are injected from outside, the vortices intensify in strengths and evolve. The evolution means that the densities in the core region increase and the spiral coiling become more and more tighter and compact. This intensification carries on as long as the rate of dissipation, or ejections from the core is balanced by the rate of inflow. During this equilibrium phase the vortices organize, and order the flows according to the pattern of the fractal geometry. However as the vortices strengthen, the equilibrium between the inflow and the outflow becomes more and more critical, and fall into more and more orderly arrangements. After reaching a critical point, the balance gets lost and the vortex core breaks down by dispersing unorganized flows in the surrounding. What happens in the global scale also repeats in the local vortices, which are embedded inside the global system. These smaller vortices also undergo the tug-of-war between the inflow and outflow, equilibrium and non-equilibrium, order and chaos. Thus an ever changing arena of fluctuating flows is generated everywhere.

When the system is critically balanced between the equilibrium and the non-equilibrium states, the breakdown and the onset of the chaos is counteracted by the formation of knotty structures, which try to halt the chaos and bring the system back to the track of orderly evolution. I shall now discuss this oscillations between order and chaos by studying the ways smaller vortices grow, interact, breakdown, and grow again in a whirlpool generated by a waterfall.

 

When the vortices are constrained to form under physical boundary conditions, like in the vortex formed by the waterfall, where the boulders have created walls restricting the flow, they develop 3D structures, which resemble knots. In situations where they develop in free space, like in the atmospheric hurricane, they tend to take a flat two-dimensional disc-like shape.

One of the most fascinating dynamics of the vortices is the formation of knots, their evolutions, which are destined to end in the breakdown of the knots, and then the mechanism of repairing the broken knots once again. The oscillations between formation and breakdown continue like heart beats of the nature. This oscillations create the ever changing unpredictable fluctuations everywhere in the entire global structure.

When flows are injected in the system it grows, and organize the streams in an orderly manner. This contracting phase creates fattened filaments, and rounder and tighter knots. This is how the vortices store energy up to a critical limit. After the critical limit is reached the knot rips open, and disperses flows in the surrounding, like a pulse, and it appears to expand. This is the way how vortices disperse local information to the global arena, and inject chaos in the global system. However, the nature reacts back to the development of the disorder by setting the process of the formation of knots again. The knots appear in order to halt the disorder, and bring the global system in orderly arrangement once more.Thus the information from the global system flows in to the local arenas to help arrange the micro structures to organize themselves in the image of the global macro-structure. This oscillation between order and disorder is finely tuned.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

The opening and the closing of the knots work as the breathing in, and the breathing out mechanism in the vortices. This is a remarkable way, by which the nature stores and transfers energies in order to regulate everything that come and go. One may ask why should the nature behave in that particular manner? May be, it is only by this mechanism the nature can recreate the cosmic design in all scales, and generate a perfect system which can perpetuate the existence of the universe.

Before leaving this chapter and going over to the comparison with the cosmic structures, I shall make a short digression about the way the vortices interact. The most common method of interactions among the vortices are to grow by feeding on each other. When a weaker vortex comes close to a stronger one the stronger vortex devours the weaker one. However, in a turbulent system which acts as an arena where many vortices of similar strengths compete with each other, the most characteristic nature of vortex interactions are breakdown of vortices by ejections. The ejected filaments, from a broken knot, merge with the neighboring vortices, which need to repair their knot structures. The interactions involving splitting and merging of filaments from one to the other, perpetuate the dynamics of vortex interactions in turbulence.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

The interactions, which constantly bring changes to the state of the vortex-knots, which bring oscillations between order and disorder in the region, provide the mechanism to channel flows in different directions. The redirections from one region to the other creates a global oscillation in the system in turn. This is also the way the local regions participate in determining the global evolution. Thus everything in a turbulence, from local happenings to the global evolutions, are inseparably inter-connected through the network of intricately woven knots and filamentary structures.

In fact, what happens in a local region can indicate what may be happening globally in the system. The best region to study turbulence is its core. The evolution of the core indicates the global evolution in the entire body. One of the most characteristic phenomenon of such evolution is the ejection of jets from the core. With this ejection the knots break and open by dispersing disorder.

 

 

 

 

 

 

 

 

 

 

As said, the evolution of the knot structure at the core is intimately correlated to the general evolutions of the vortices everywhere through the turbulent structure. The present study shows that when the knot, which forms at the core, becomes tighter it suddenly collapses, and undergoes drastic changes in shape. In this process it ejects smaller knot from the centre as ejecta. After that the core relaxes for a while before it starts building up the knot once again. This tightening and relaxation of the central core corresponds to the phase of the global order and disorder. The system acts as a organic whole, where all parts seem to know what are happening in other parts and can act simultaneously. This is very different from the laws of science which we know today.